Iris Flower Classification: A Machine Learning Project with SVM Optimization in Python

In this project we use the famous Iris dataset, one of the most widely used datasets in machine learning. It contains 150 flower samples, equally distributed among three species: setosa, versicolor, and virginica. Each flower is described by four numerical features:

  • Sepal length (cm) — The length of the sepal.
  • Sepal width (cm) — The width of the sepal.
  • Petal length (cm) — The length of the petal.
  • Petal width (cm) — The width of the petal.

The goal is to build a classification model that predicts the flower species based on these features. To achieve this, we use a Support Vector Machine (SVM) classifier with a pipeline that includes:

  • Data preprocessing — Features are standardized using StandardScaler.
  • Model selection — An SVM with an RBF kernel is trained.
  • Hyperparameter tuning — The parameters C and gamma are optimized using GridSearchCV with cross-validation.
  • Performance tracking — Performance is measured with accuracy, precision, recall, F1-score, and confusion matrices.

Import packages

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import (accuracy_score, classification_report, confusion_matrix, 
                           ConfusionMatrixDisplay, precision_score, recall_score, f1_score)
from sklearn.pipeline import Pipeline

Load dataset and Create dataframe

data = load_iris()
X, y = data.data, data.target
feature_names = data.feature_names
target_names = data.target_names

df = pd.DataFrame(X, columns=feature_names)
df['target'] = y
df['species'] = df['target'].map({0: 'setosa', 1: 'versicolor', 2: 'virginica'})

print(f"Dataset Dimensions: {X.shape}")
print(f"Available Characteristics: {feature_names}")
  • Dataset Dimensions: (150, 4)
  • Available Characteristics: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

    • Train-Test

    X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42, stratify=y
)

print(f"Training Variable: {X_train.shape[0]} samples")
print(f"Testing Variable: {X_test.shape[0]} samples")
    As the test size is 0.2 (20%) and the number of samples is 150:
  • Training Variable: 120 samples
  • Testing Variable: 30 samples

    • Pipeline for SVM

    svm_pipeline = Pipeline([
    ('scaler', StandardScaler()),
    ('svm', SVC(kernel='rbf', random_state=42, probability=True))
])

    Optimal hyperparameter search

    svm_param_grid = {
    'svm__C': [0.1, 1, 10, 100],
    'svm__gamma': [0.001, 0.01, 0.1, 1, 'scale']
}
    Hyperparameters:
  • C (Regularization Strength): Controls the trade-off between maximizing the margin and minimizing classification errors. Tested values: [0.1, 1, 10, 100]
  • γ (Gamma - Kernel Coefficient): Defines the reach of each training example's influence in the RBF kernel. Tested values: [0.001, 0.01, 0.1, 1] with the purpose of scaling the kernel's influence proportionally
  • These two formulas will be used: RBF Kernel (Radial Basis Function) and SVM Loss Function with L2 Regularization

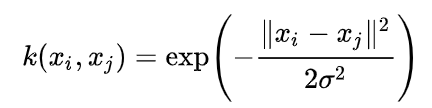
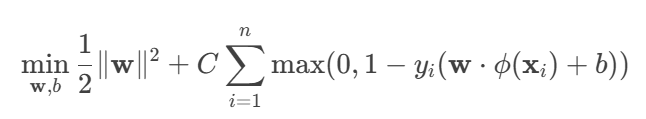
    • RBF Kernel

    • xi, xj: data vectors (training samples).
    • ‖xi - xj‖2: squared Euclidean distance between the two points.
    • σ: controls the width of the Gaussian.
    • k(xi, xj): similarity measure (1 = similar, 0 = far apart)

    In SVM Loss with L2 Regularization:

    • w: weight vector of the hyperplane.
    • b: bias term.
    • ‖w‖2: L2 regularization term (penalizes large weights).
    • C: trade-off parameter between margin size and correct classification.
    • n: number of samples.
    • yi: label of sample i (1 or -1).
    • φ(xi): feature transformation of xi (done by the RBF kernel).
    • max(0, 1 - yi(…)): hinge loss (penalty if a sample is misclassified or too close to the margin).

    Best SVM model

    svm_grid = GridSearchCV(svm_pipeline, svm_param_grid, cv=5)
svm_grid.fit(X_train, y_train)
best_svm = svm_grid.best_estimator_
y_pred_svm = best_svm.predict(X_test)
y_pred_proba_svm = best_svm.predict_proba(X_test)
    This code tunes an SVM model via grid search with 5-fold CV, fits it to training data, gets the best estimator, and predicts labels and probabilities on test data.

    Create subplots and set the figure size

    figura = plt.figure(figsize=(22, 16))
colors = {'setosa':'red', 'versicolor':'green', 'virginica':'blue'}
ax2 = figura.add_subplot(111, projection='3d')
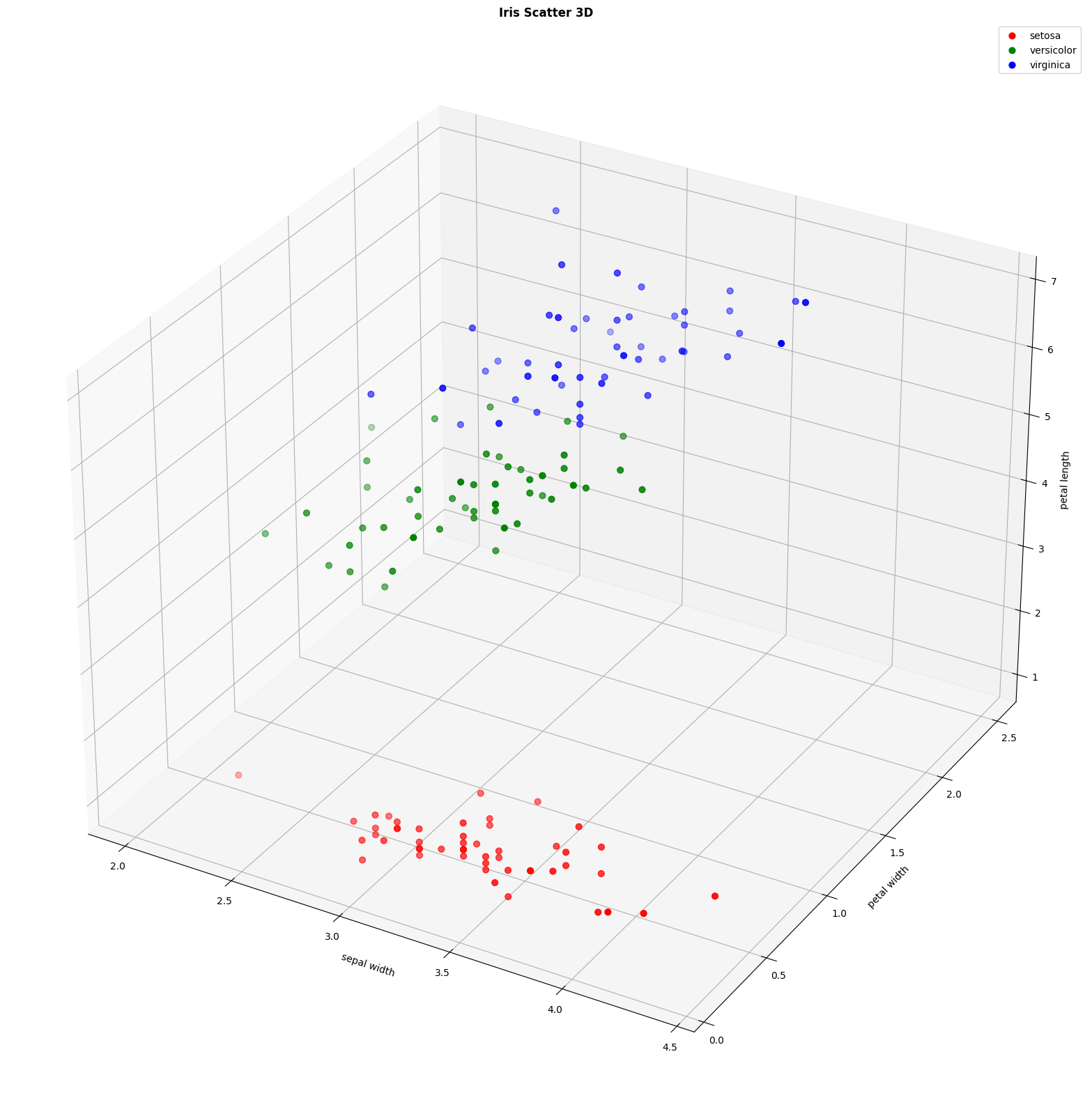
for specie, df in df.groupby('species'):
	ax2.scatter(df['sepal width (cm)'], df['petal width (cm)'], df['petal length (cm)'], c=colors[specie], label=specie, s=40)
ax2.set_xlabel("sepal width")
ax2.set_ylabel("petal width")
ax2.set_zlabel("petal length")
ax2.set_title("Iris Scatter 3D", fontweight='bold')
ax2.legend()

fig, axes = plt.subplots(2, 2, figsize=(15, 12))

# Confusion matrix
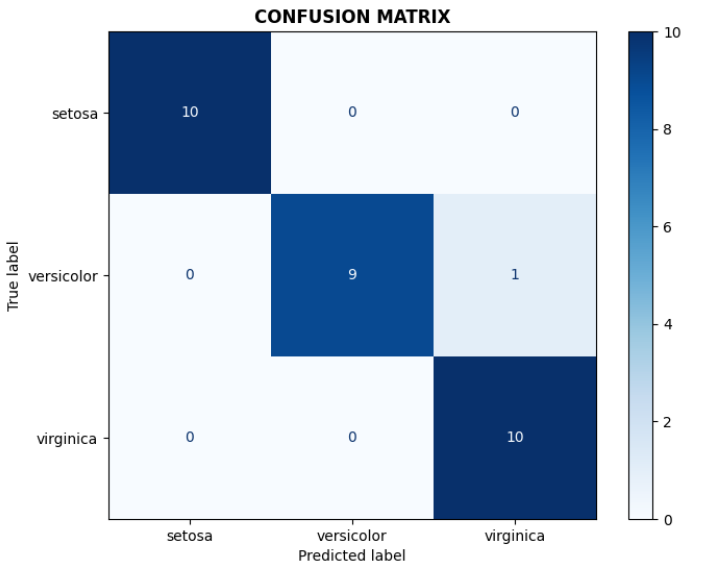
cm = confusion_matrix(y_test, y_pred_svm)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=target_names)
disp.plot(ax=axes[0,0], cmap='Blues')
axes[0,0].set_title('CONFUSION MATRIX', fontweight='bold')

# Correlation matrix located in axes[0,1]
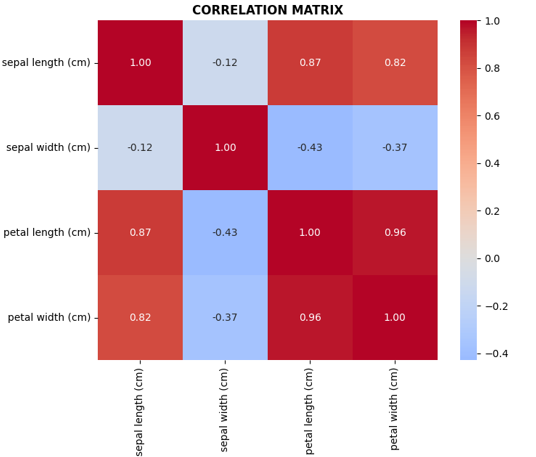
corr_matrix = df[['sepal length (cm)', 'sepal width (cm)', 
                  'petal length (cm)', 'petal width (cm)']].corr()
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', center=0, 
            ax=axes[0,1], fmt='.2f', square=True)
axes[0,1].set_title('CORRELATION MATRIX', fontweight='bold')

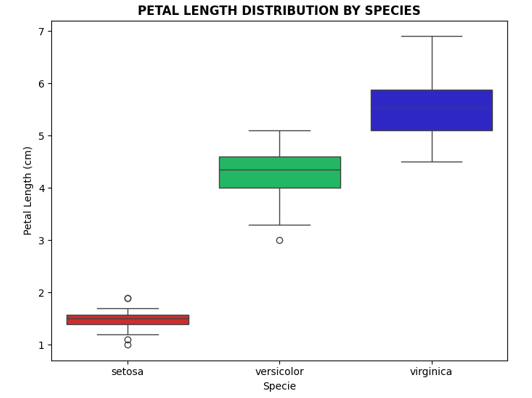
# Petal length distribution located in axes[1,0]
sns.boxplot(x='species', y='petal length (cm)', data=df, ax=axes[1,0], 
            hue='species',
            palette=["#E61313", "#0CCF60", "#170DDF"],
            legend=False)
axes[1,0].set_title('PETAL LENGTH DISTRIBUTION BY SPECIES', fontweight='bold')
axes[1,0].set_ylabel('Petal Length (cm)')
axes[1,0].set_xlabel('Specie')

# Sepal width distribution located in axes[1,1]
sns.histplot(data=df, x='sepal width (cm)', hue='species', 
             ax=axes[1,1], palette=['#E61313', '#0CCF60', '#170DDF'], 
             alpha=0.6, element='step', kde=True)
axes[1,1].set_title('SEPAL WIDTH DISTRIBUTION BY SPECIES', fontweight='bold')
axes[1,1].set_xlabel('Sepal Width (cm)')

# Last step of creating subplots
plt.tight_layout()
plt.show()

    Accuracy results

    print(f"Cross-validation accuracy: {svm_grid.best_score_:.5f}")
print(f"Test set accuracy: {accuracy_score(y_test, y_pred_svm):.5f}")
    Regarding accuracy results we have:
  • Cross-validation accuracy = 0.97500
  • Test set accuracy = 0.96667

    • Metrics by class

    precision = precision_score(y_test, y_pred_svm, average=None)
recall = recall_score(y_test, y_pred_svm, average=None)
f1 = f1_score(y_test, y_pred_svm, average=None)

report = classification_report(y_test, y_pred_svm, target_names=target_names, digits=5)
print(f"{report}")

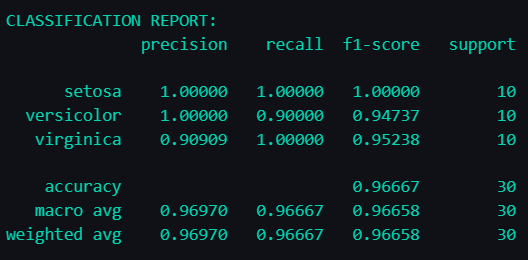
    The empty cells in the "accuracy" row (under precision and recall) exist because accuracy is a single overall metric for the model, not broken down by those categories.

    Final Output

    results_df = pd.DataFrame({
    'Real': y_test,
    'Prediction': y_pred_svm,
    'Correct': y_test == y_pred_svm
})

results_df['Real_Especie'] = results_df['Real'].map({0: 'setosa', 1: 'versicolor', 2: 'virginica'})
results_df['Pred_Especie'] = results_df['Prediction'].map({0: 'setosa', 1: 'versicolor', 2: 'virginica'})

print(f"NUMBER OF CORRECT PREDICTIONS: {results_df['Correct'].sum()}/{len(results_df)}")
print(f"FINAL ACCURACY: {accuracy_score(y_test, y_pred_svm):.5f}")
print(f"BEST HYPERPARAMETERS: {svm_grid.best_params_}")

    We finally have:

    • Number of correct predictions: 29/30
    • Final accuracy: 96.667% (0.96667)
    • Best hyperparameters:
      • C: 1
      • γ: 0.1

    Conclusions

    • Petal features are more discriminative than sepal features
    • The SVM model achieves high accuracy in multiclass classification
    • The species setosa is the easiest to classify, however, versicolor and virginica show some overlap

    This project demonstrates how machine learning can extract meaningful patterns, in this specific case, from botanical data. Could we apply this same approach to your classification challenge? Let's connect to discuss how SVM or other ML models could solve your business problems.

    View Full Code on GitHub